Fea: il Dimensionamento dei recipienti in pressione
L'analisi degli elementi finiti rappresenta un metodo numerico che si basa sulla modellizzazione di un problema fisico, allo scopo di poter ottenere un sistema di equazioni differenziali, caratterizzato da un numero finito di incognite. In particolare l'analisi agli elementi finiti applicata al caso dei recipienti in pressione - sottoposti a carichi esterni - permette di calcolare il loro dimensionamento.
L'idea fondamentale per un qualunque metodo di discretizzazione delle equazione alle derivate parziali EDP, è quello di discretizzare un dato problema continuo - con infiniti gradi di libertà - per ottenere un problema discreto; questo è un sistema di equazioni con un numero finito di incognite che può essere risolto tramite l'impiego di un calcolatore.
Le equazioni alle derivate parziali forniscono modelli matematici di tanti diversi problemi fisici - presenti in ambito ingegneristico - come nel caso dei problemi di idrodinamica.
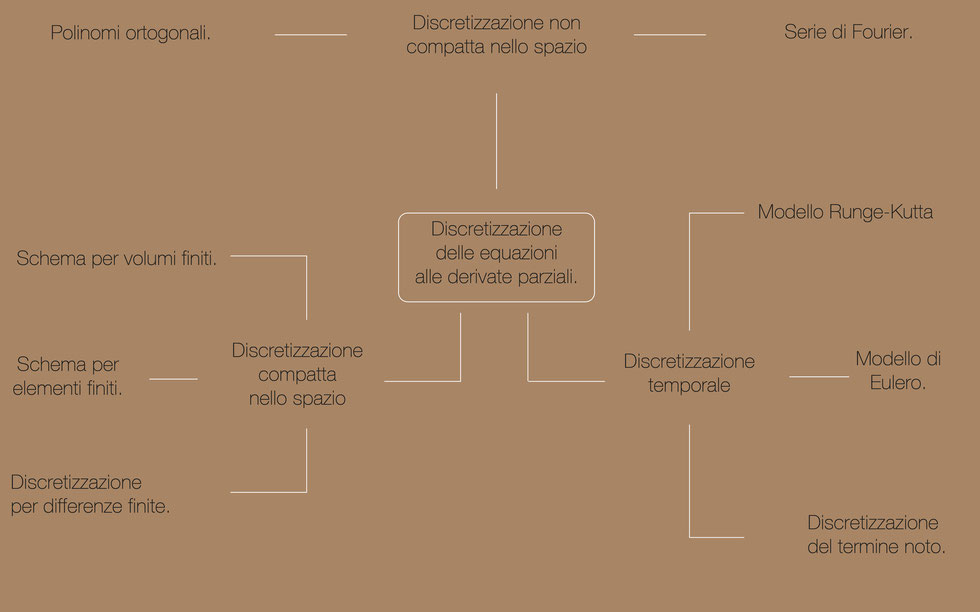
In particolar modo la discretizzazione delle equazioni alle derivate parziali può essere di tre tipi diversi, compatta nello spazio, non compatta nello spazio, e di tipo temporale; ai quali corrispondono diversi metodi risolutivi.
Per quanto riguarda la discretizzazione non compatta nello spazio, possiamo dire che esistono due tipi di soluzioni: la serie di Fourier, e i polinomi ortogonali. Abbiamo poi la discretizzazione compatta nello spazio, a cui seguono tre tipi di soluzioni: Schema per volumi finiti, Schema per elementi finiti, e discretizzazione per differenze finite.
Infine consideriamo la Discretizzazione temporale, caratterizzata da tre tipi di soluzioni: modello Runge-Kutta, modello di Eulero, e Discretizzazione del termine fonte.
La soluzione numerica delle equazioni richiede la discretizzazione delle equazioni alle derivate parziali. La prima questione è: possiamo rappresentare in maniera discreta una funzione continua?
La maniera più semplice sembra essere quella di definire una maglia su di una griglia (che noi supponiamo 1-d e regolare) e di definire la funzione f per il valore che essa prende in corrispondenza dei nodi della griglia.
Queste equazioni differenziali possono essere classificate in base alla loro formulazione matematica in tre famiglie diverse:
- ellittiche,
- iperboliche,
- paraboliche
per ognuna delle quali bisogna considerare un metodo numerico specifico. Nella scelta del metodo numerico intervengono diverse caratteristiche come la velocità di convergenza e il costo computazionale.